hdu 6626 geometric problem(解析几何)

很容易读懂的几何题，就是非常非常难写。

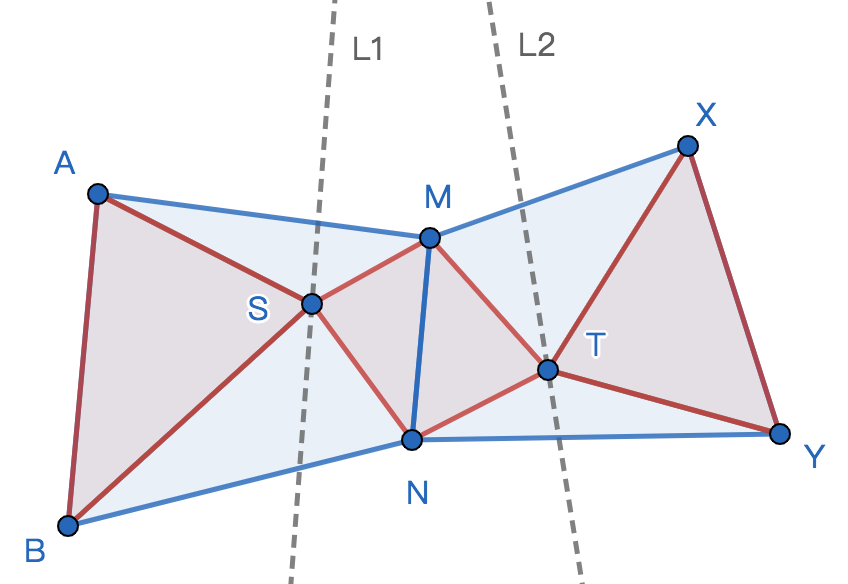
要求ABS与SNTM与XYT三个图形面积相同，并且S和T分别在直线L1、L2上，并且在对应的四边形内部。输出S和T的解，若有多个，输出字典序最小的(先S的x坐标，再S的y坐标这样)。

直观来看，在非退化情形下，S和T均有一个移动的自由度，而面积有两条方程限制，应该是有唯一解的，所以只要列方程求解再判断是否满足条件即可。

而对于特殊情形，比如L1与AB边平行，这时候方程可能无解或无数解。字典序最小的解无非出现在L1、L2与各个边的交点处，所以把可能的交点全部加入再判断面积是否相等。

具体实现来说，我在S和T上各设了一个参变量，然后用定比分点算距离，再解方程。但是貌似不比标程直接高斯消元简单。

```
#include <bits/stdc++.h>
```
```
using namespace std;
```
```
 
```
```
typedef long long ll;
```
```
 
```
```
typedef double db;
```
```
const db PI=acos(-1);
```
```
const db eps=1e-10, inf=1e12;
```
```
 
```
```
bool eq(db x){return fabs(x)<eps;}
```
```
int sgn(db x){
```
```
    if (x<=-eps) return -1;
```
```
    return x>=eps;
```
```
}
```
```
 
```
```
#define Vec const vec &
```
```
#define Point const point &
```
```
struct vec{
```
```
    db x,y;
```
```
    vec():x(0),y(0){}
```

    vec(db x, db y):x(x),y(y){} //[i] init-list is easier to use in c++1x

    vec(db theta):x(cos(theta)),y(sin(theta)){}

```
 
```

    bool operator==(Vec v) const{return eq(x-v.x) && eq(y-v.y);}

```
    db ang() const{return atan2(y,x);}
```
```
 
```

    vec operator+(Vec v) const{return vec(x+v.x,y+v.y);}

    vec operator-(Vec v) const{return vec(x-v.x,y-v.y);}

    vec operator*(db a) const{return vec(x*a,y*a);}

    vec operator/(db a) const{return vec(x/a,y/a);}

```
 
```

    db operator|(Vec v) const{return x*v.x+y*v.y;} //dot

    db operator&(Vec v) const{return x*v.y-y*v.x;} //cross

    db operator!() const{return sqrt(x*x+y*y);}    //len

    db operator~() const{return x*x+y*y;}    //len

```
 
```

    bool operator<(Vec v) const{return x==v.x?y<v.y:x<v.x;}

```
    //rotate countclockwise
```

    vec std() const{return *this/!*this;}

    vec rot(db rad) const{return vec(x*cos(rad)-y*sin(rad), x*sin(rad)+y*cos(rad));}

```
    vec l90() const{return vec(-y,x);}
```
```
    vec r90() const{return vec(y,-x);}
```

    vec vert() const{return (*this).l90().std();}  //l90 and standard

```
 
```
```
    void rd(){scanf("%lf%lf",&x,&y);}
```

    void prt(){printf("%.10f %.10f",x,y);}

    friend ostream& operator<<(ostream &o, Vec v){return o<<v.x<<','<<v.y;}

```
};
```
```
typedef vec point;
```

db cross(Vec a, Vec b, Vec c){return b-a&c-a;}

db dot(Vec a, Vec b, Vec c){return b-a|c-a;}

point lineInt(Point p, Vec vp, Point q, Vec vq){

```
    db t=(vq & p-q)/(vp&vq);
```
```
    return p+vp*t;
```
```
}
```
```
db lineDis(Point p, Point s, Vec v){
```
```
    return (v & p-s)/!v;
```
```
}
```
```
 
```
```
int main(){
```
```
    int T; cin>>T;
```
```
    while (T--){
```

        point A,B,M,N,X,Y,L11,L12,L21,L22;

        A.rd(); B.rd(); M.rd(); N.rd(); X.rd(); Y.rd();

```
        if (cross(A,B,M)<0) swap(A,B);
```
```
        if (cross(M,N,X)<0) swap(M,N);
```
```
        if (cross(Y,X,M)<0) swap(X,Y);
```

        L11.rd(); L12.rd(); L21.rd(); L22.rd();

```
        L12=L12-L11;
```
```
        L22=L22-L21;
```
```
        point C11=L11-L12*2;
```
```
        point C12=L11+L12*2;
```
```
        point C21=L21-L22*2;
```
```
        point C22=L21+L22*2;
```

        //w1 x + b1 = w2 x + w3 y + b2 = w4 y + b3

```
        //(t d1 + (1-t) d2) / l0
```
```
        db w1, w2, w3, w4, b1, b2, b3;
```
```
        db d1=lineDis(C11,A,B-A);
```
```
        db d2=lineDis(C12,A,B-A);
```
```
        db l0=!(B-A);
```
```
        w1=(d1-d2)*l0;
```
```
        b1=d2*l0;
```
```
        d1=-lineDis(C11,M,N-M);
```
```
        d2=-lineDis(C12,M,N-M);
```
```
        l0=!(M-N);
```
```
        w2=(d1-d2)*l0;
```
```
        b2=d2*l0;
```
```
        d1=lineDis(C21,M,N-M);
```
```
        d2=lineDis(C22,M,N-M);
```
```
        w3=(d1-d2)*l0;
```
```
        b2+=d2*l0;
```
```
        //cout<<w3*0.5625+d2*l0<<'\n';
```
```
        d1=-lineDis(C21,X,Y-X);
```
```
        d2=-lineDis(C22,X,Y-X);
```
```
        l0=!(Y-X);
```
```
        w4=(d1-d2)*l0;
```
```
        b3=d2*l0;
```
```
        //(w1-w2)x - w3 y= +b2-b1
```
```
        //- w2 x+(w4-w3)y= +b2-b3
```
```
        bool hx=0, hy=0;
```
```
        db det=(w1-w2)*(w4-w3)-w2*w3;
```

        db dex=(b2-b1)*(w4-w3)+w3*(b2-b3);

        db dey=(b2-b3)*(w1-w2)+w2*(b2-b1);

```
        vec ansx, ansy;
```
```
        if (eq(det)){
```
```
            if (eq(dex) && eq(dey)){
```
```
                hx=1,hy=1;
```
```
            }
```
```
            else goto fail;
```
```
        }
```
```
        if (!hx && !hy) {
```
```
            db x=dex/det,y=dey/det;
```

            ansx=C11*x+C12*(1-x),ansy=C21*y+C22*(1-y);

            if (cross(B,ansx,A)<-eps || cross(N,ansx,B)<-eps || cross(M,ansx,N)<-eps || cross(A,ansx,M)<-eps) goto fail;

            if (cross(M,ansy,X)<-eps || cross(N,ansy,M)<-eps || cross(Y,ansy,N)<-eps || cross(X,ansy,Y)<-eps) goto fail;

            ansx.prt(); putchar(' '); ansy.prt(); puts("");

```
        }
```
```
        if (hx || hy){
```

        point P11=lineInt(L11,L12,A,M-A);

        point P12=lineInt(L11,L12,B,N-B);

        point P21=lineInt(L21,L22,X,M-X);

        point P22=lineInt(L21,L22,Y,N-Y);

            vector<pair<point,point> > ans;

```
            bool f11,f12,f21,f22;
```
```
            f11=f12=f21=f22=1;
```

            if (dot(A,P11,M)*dot(M,P11,A)>0) f11=1; else P11=lineInt(L11,L12,M,M-N);

            if (dot(B,P12,N)*dot(B,P12,N)>0) f12=1; else P12=lineInt(L11,L12,M,M-N);

            if (dot(M,P21,X)*dot(X,P21,M)>0) f21=1; else P21=lineInt(L21,L22,M,M-N);

            if (dot(N,P22,Y)*dot(Y,P22,N)>0) f22=1; else P22=lineInt(L21,L22,M,M-N);

            if (f11 && f21) ans.push_back({P11,P21});

            if (f11 && f22) ans.push_back({P11,P22});

            if (f12 && f21) ans.push_back({P12,P21});

            if (f12 && f22) ans.push_back({P12,P22});

```
            if (!eq(w1-w2)){
```
```
                if (f11){
```

                    db x=1-(P11-C11|C12-C11)/~(C12-C11);db y=(b2-b1-(w1-w2)*x)/(-w3);

                    ans.push_back({P11,C21*y+C22*(1-y)});

```
                }
```
```
                if (f12){
```

                    db x=1-(P12-C11|C12-C11)/~(C12-C11);db y=(b2-b1-(w1-w2)*x)/(-w3);

                    ans.push_back({P12,C21*y+C22*(1-y)});

```
                }
```
```
            }
```
```
            if (!eq(w4-w3)){
```
```
                if (f21){
```

                    db y=1-(P21-C21|C22-C21)/~(C22-C21);db x=(b2-b3-(w4-w3)*y)/(-w2);

                    ans.push_back({C11*x+C12*(1-x),P21});

                    //point t=C11*x+C12*(1-x);

                    //printf("%f %f %f\n",cross(X,P21,Y),cross(N,M,t),cross(M,N,P21));

```
                }
```
```
                if (f22){
```

                    db y=1-(P22-C21|C22-C21)/~(C22-C21);db x=(b2-b3-(w4-w3)*y)/(-w2);

                    ans.push_back({C11*x+C12*(1-x),P22});

```
                }
```
```
            }
```

            auto pc=remove_if(ans.begin(),ans.end(),[&](const pair<point,point> &e){

```
                return 
```

                cross(B,e.first,A)<-eps || cross(N,e.first,B)<-eps || cross(M,e.first,N)<-eps || cross(A,e.first,M)<-eps ||

                cross(M,e.second,X)<-eps || cross(N,e.second,M)<-eps || cross(Y,e.second,N)<-eps || cross(X,e.second,Y)<-eps ||

                !eq(cross(A,B,e.first)-cross(X,e.second,Y))||!eq(cross(A,B,e.first)-cross(N,M,e.first)-cross(M,N,e.second));

```
            });
```
```
            ans.erase(pc,ans.end());
```
```
            if (ans.empty()) goto fail;
```

            sort(ans.begin(),ans.end());

            ans[0].first.prt(); putchar(' '); ans[0].second.prt(); puts("");

```
        }
```
```
        continue;
```
```
        fail:
```
```
        puts("-1");
```
```
    }
```

fffasttime

hdu 6626 geometric problem(解析几何)

发表评论取消回复

发表评论 取消回复

发表评论取消回复